- Triangulation
Triangulation. Zur Aufnahme großer Gebiete, als Unterlage für technische Messungen und zur Verbindung von Einzelmessungen führt man zusammenhängende Dreiecksmessungen aus. Man gibt den Dreieckspunkten eine dauernde Vermarkung, mißt eine Grundlinie, im übrigen nur Winkel, rechnet geographische und ebene Koordinaten für die Eckpunkte und nimmt diese Werte als Ausgang für alle weiteren Messungen.
Im Eisenbahnbau werden T. zur Festlegung der Achse längerer Tunnel durchgeführt, namentlich bei sog. Scheiteltunneln, weil hier die Aussteckung der Tunnelachse im Gelände der großen Überlagerung wegen nicht angängig ist.
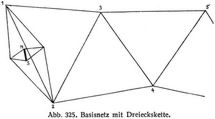
Im großen werden die Dreiecksmessungen durch die Landesaufnahme ausgeführt. An sorgfältig ausgewählter und vorbereiteter Stelle wird mit hoher Genauigkeit eine Grundlinie, die Basis, gemessen, aus ihr leitet man durch Winkelmessung in rautenförmigem Basisnetz eine mehrfach längere Dreiecksseite ab, wobei besonders die spitzen Winkel mit großer Schärfe zu messen sind, und schließt durch Winkelmessung weitreichende Dreiecksketten an. Ein mit der Kette verbundener Punkt ist durch astronomische Messungen nach geographischer Breite und Länge zu bestimmen, auf gleichem Wege ist das Azimut einer Dreiecksseite festzulegen. Die Basis wird 2–8 km, die aus ihr abgeleitete Dreiecksseite 5- oder 6 mal so lang genommen. In und zwischen die Dreiecksketten werden Füllnetze mit stufenweise kleineren Seiten gelegt. Die Dreiecke erster Ordnung haben Seiten von 25–75 km, gelegentlich bis über 100 km, die zweiter Ordnung von 15 bis 20 km, die dritter Ordnung von 3–5 km. Für die Dreiecke ist möglichst gleichseitige Form anzustreben.
Die Basismessung größter Genauigkeit erfordert viel Gehilfen und umfangreiche Meßvorrichtungen. Mit dem Basismeßapparat von Bessel oder von Brunner erreicht man innere Genauigkeiten von etwa 2/3 mm der einfach gemessenen km-Länge; die absolute Genauigkeit ist wegen systematischer Fehlereinflüsse, vor allem der Temperatur, viel geringer. Neuerdings sucht man nicht mehr die Genauigkeit der Längenmessung zu steigern, da sie durch die unvermeidlichen Fehler der Winkelmessung in den Dreiecken doch bald wieder verloren geht; vielmehr legt man, um der fortschreitenden Fehlerwirkung der Winkelmessungen zu begegnen, in bestimmten Abständen, alle 200 bis 300 km, eine neue Basis ein. Jetzt begnügt man sich vielfach auch mit geringerer Genauigkeit der Längenmessung, etwa 2 mm Unsicherheit auf 1 km einfach gemessener Länge, die man nach dem Verfahren von Jäderin mit Meßdrähten erreichen kann. Statt Drähten aus verschiedenem Metall zur Berücksichtigung des Temperatureinflusses werden jetzt durchweg Drähte aus Invar – 64% Stahl, 36% Nickel – genommen, die in diesem Mischungsverhältnis einen bis 100mal kleineren Koeffizienten der Wärmeausdehnung haben als Eisen. Die Neigung der Invardrähte zu sprungweiser Längenänderung wird durch monatelange Behandlung vor der Verwendung beseitigt; die Längung der Drähte wird dadurch berücksichtigt, daß man die Drähte vor und nach der Basismessung eicht, wozu die Hilfsbasis des geodätischen Instituts in Potsdam eingerichtet ist. Man verwendet nebeneinander 2 bis 4 Drähte zu einer Basismessung. Die gemessene Basislänge ist auf den Landesvermessungshorizont zu reduzieren.
Die Winkelmessung bei der Großtriangulierung wird mit Schraubenmikroskop-Theodoliten ausgeführt. Zur Kleintriangulierung kann man auch Nonien-Theodolite mit Repetitionseinrichtung benutzen. Die Sichtbarmachung der Dreieckspunkte geschieht durch Signale, Stangen und Pyramiden, auf große Entfernung unter Verwendung von Heliotroplicht oder elektrischem Licht. Wenn zur Oberwindung der Erdkrümmung oder von Sehhindernissen der Theodolit auf einen Hochstand gestellt werden muß, so ist der Instrumentenpfeiler fest und erschütterungsfrei zu bauen, also vollständig getrennt vom Beobachterstand und Leuchtstand oder der Zielspitze zu erstellen; die beiden Holzpyramiden dürfen einander nicht berühren. Die Genauigkeit der Winkelmessung ist so zu bemessen, daß die Koordinatenwerte der Dreieckspunkte gegeneinander auf etwa 1 dm sicher sind.
Für die Landesaufnahmen rechnet man für die Dreieckspunkte geographische und rechtwinklig sphäroidische Koordinaten. Bei uns werden für das Erdellipsoid die von Bessel abgeleiteten Werte: große Halbachse a = 6,377.397 m, kleine b = 6,356.079 m, Abplattung 1 : 299 angenommen. In kleineren Vermessungsgebieten bezieht man die Berechnungen auf die Schmiegungskugel der Mitte des Gebiets. Die rechtwinkligen Koordinaten rechnet man in Meridianstreifen von 3° Breite, früher im Cassini-Soldnerschen Koordinatensystem, jetzt in konformen Koordinaten nach Gauß. Man verwendet dazu das Verfahren von Krüger der unmittelbaren konformen Abbildung des Ellipsoids auf die Ebene. Bei der Kleintriangulierung rechnet man, wie bei der Kleinmessung überhaupt, nur nach ebenen Koordinaten.
Für Ingenieurarbeiten wird man, wenn eine Landesaufnahme vorhanden ist, von dieser ausgehen und die Dreiecksmessung nach Bedarf weiter ins kleine treiben. Liegt aber eine solche Aufnahme nicht vor, so wird man sich eine selbständige Dreiecksmessung anlegen und im kleinen ähnlich verfahren wie die Landesaufnahme im großen. Man mißt an günstiger Stelle eine Grundlinie von einigen hundert Metern Länge. Hierzu kann man Invardrähte verwenden. Meist aber werden gute 5 m-Latten genügen, mit Neigungsmesser, wenn nur täglich vor und nach jeder Messung die Längen der Latten mit Normalmaßen geprüft werden. Man erhält mit dieser Lattenmessung einen mittleren Fehler von 2–3 cm der einfach gemessenen km-Strecke. Zur Winkelmessung wird im allgemeinen der Nonien-Theodolit genügen, da bei Horizontabgleichung der vierfach repetierte Winkel bis auf wenige Sekunden genau erhalten wird. Auf diese Weise läßt sich die selbständige Dreiecksmessung des Ingenieurs in einfacher Weise ausführen. Eine größere Sorgfalt erfahren die Dreiecksmessungen für die Gegenortsbetriebe großer Tunnels, die deshalb schwierig durchzuführen sind, weil sie meist im Hochgebirge vorkommen und bis in enge Täler hineinzubringen sind. Bei der Absteckung großer Alpentunnel der zweiten Eisenbahnverbindung Wien-Triest hat Tichy als Basislinie nur einen 1∙2 m langen Invarstab genommen.
Literatur: Veröffentlichungen der Landesaufnahmen der verschiedenen Länder. – Jordan, Handbuch der Vermessungskunde, Bd. II und III, Feldmessung, Landesvermessung und Erdmessung (mit großer Literaturangabe). – Dolezalek, Durchschlag und Richtungsbestimmung des Gotthard-Tunnels. Ztschr. d. Arch. u. Ing.-Vereins zu Hannover 1880. – Koppe, Bestimmung der Achse des Gotthard-Tunnels. Ztschr. f. Vermess.-Wesen 1875 und 1876. – Gelpke, Bestimmung der Gotthard-Tunnelachse. Zivilingenieur 1870. – Rosenmund, Absteckung des Simplon-Tunnels. Schwz. Bauztg. 1901. – Baeschlin, Absteckung des Lötschberg-Tunnels. Schwz. Bauztg. 1911, Bd. LVIII. – Schumann, Lotstörungen und ihre Anwendung bei Tunnelabsteckungen. Ztschr. d. Österr. Ing.-V. – Tichy, Messung von Grundlinien genauer als mit optischtachymetrischem Verfahren, wo die gebräuchlichen Methoden versagen. Wien 1909.
Haußmann.
http://www.zeno.org/Roell-1912. 1912–1923.